1  Introducción a los modelos de regresión

Este tema inaugural tiene como misión construir el andamiaje conceptual y filosófico sobre el que se asienta el modelado estadístico moderno. A lo largo de estas páginas, contextualizaremos la regresión no solo como una técnica, sino como un marco de pensamiento indispensable en la ciencia de datos y en cualquier disciplina de investigación cuantitativa. Exploraremos en profundidad su propósito dual, desgranaremos sus componentes axiomáticos hasta el último detalle, y ofreceremos una visión panorámica, rica en matices, de la vasta familia de modelos de regresión. El objetivo es preparar al lector, con solidez y sin prisas, para las inmersiones técnicas que seguirán en los capítulos posteriores. Como lectura complementaria que comparte esta filosofía de aprendizaje profundo pero aplicado, recomendamos encarecidamente la obra de (James et al. 2021).

1.1 Predecir vs. explicar

El modelado de regresión constituye una de las herramientas más potentes y flexibles del arsenal estadístico. Ofrece un marco metodológico riguroso para investigar y cuantificar las relaciones entre un conjunto de variables, y su aplicabilidad abarca un espectro extraordinariamente amplio de disciplinas: desde la física de partículas y la ingeniería aeroespacial, donde se usa para modelar sistemas complejos, hasta la econometría, la psicometría, la epidemiología o las finanzas, donde es fundamental para entender mercados y comportamientos.

Aunque en la práctica ambos objetivos a menudo se entrelazan, conceptualmente, el modelado estadístico se orienta hacia uno de dos polos, una dicotomía fundamental articulada brillantemente por (Shmueli 2010): la predicción o la inferencia (explicación). Comprender esta distinción es el primer paso para convertirse en un modelador eficaz.

  1. Predicción: El objetivo principal es la precisión. Se busca construir un modelo que pueda estimar con el menor error posible el valor de una variable de interés (la respuesta) basándose en la información proporcionada por otras variables (las predictoras). En este paradigma, el modelo puede ser tratado como una “caja negra” (black box). Su funcionamiento interno o la interpretabilidad de sus componentes son secundarios, siempre y cuando sus predicciones sean consistentemente fiables y robustas en datos no observados previamente.

Una entidad financiera quiere predecir la probabilidad de que un cliente incurra en impago de un crédito. Utilizan variables como la edad, ingresos, nivel de estudios y historial crediticio. El banco no necesita necesariamente entender la “causa” exacta del impago; su principal interés es tener un modelo que clasifique correctamente a los futuros solicitantes como de alto o bajo riesgo para minimizar pérdidas.

  1. Inferencia: El foco se desplaza radicalmente hacia la comprensión y la interpretación. El objetivo no es solo predecir, sino dilucidar la naturaleza de las interdependencias entre las variables. Se busca cuantificar cómo un cambio en una variable predictora influye, ya sea de forma causal o asociativa, en la variable de respuesta. Aquí, la interpretabilidad del modelo es primordial. El interés reside en la magnitud, el signo y, crucialmente, la incertidumbre estadística (expresada mediante errores estándar, intervalos de confianza y p-valores) de los parámetros estimados.

Una epidemióloga investiga los factores de riesgo de una enfermedad cardíaca. Modela la presión arterial en función de variables como el índice de masa corporal (IMC), el consumo diario de sal y las horas de ejercicio semanales. Su objetivo no es solo predecir la presión arterial de un paciente, sino entender y cuantificar la relación: “¿En cuántos mmHg aumenta la presión arterial, en promedio, por cada gramo adicional de sal consumido al día, manteniendo constantes el IMC y el ejercicio?”. La respuesta a esta pregunta tiene implicaciones directas para la salud pública y las recomendaciones dietéticas.

ImportanteUna relación simbiótica

Aunque conceptualmente distintos, ambos objetivos no son mutuamente excluyentes; a menudo se benefician el uno del otro. Un modelo con una base inferencial sólida, que captura relaciones causales o asociativas verdaderas, suele tener un buen rendimiento predictivo. A la inversa, un modelo que demuestra una alta precisión predictiva en datos nuevos nos da confianza en que las relaciones que ha aprendido no son meras casualidades del conjunto de datos de entrenamiento, sino que probablemente reflejen patrones reales y generalizables. La tensión entre interpretabilidad y precisión es uno de los debates más fascinantes en la ciencia de datos moderna.

1.2 Anatomía de un modelo de regresión: los componentes axiomáticos

Todo modelo de regresión, desde el más simple hasta el más sofisticado, se construye sobre tres pilares fundamentales. Estos componentes, definidos en textos clásicos como el de (Kutner et al. 2005), son los ladrillos con los que edificaremos todo nuestro conocimiento.

1.2.1 La variable de respuesta

También designada como variable dependiente, variable de salida, target, variable objetivo o variable explicada. Representa el fenómeno o la característica principal cuyo comportamiento se busca modelar, comprender o predecir. La naturaleza de esta variable es, quizás, el factor más determinante a la hora de elegir el tipo de modelo de regresión. Puede ser:

  • Continua: Una variable que puede tomar cualquier valor dentro de un rango. Ej: temperatura, altura, precio de una acción, concentración de un compuesto químico.
  • Discreta de Conteo: Una variable que representa un número de eventos. Ej: número de accidentes en una intersección, número de clientes que entran en una tienda, número de mutaciones en un gen.
  • Binaria o Dicotómica: Una variable con solo dos resultados posibles. Ej: éxito/fracaso, enfermo/sano, compra/no compra, spam/no spam.
  • Categórica: Una variable que representa grupos o categorías. Si no tiene orden, es nominal (ej: tipo de sangre, partido político); si tiene un orden intrínseco, es ordinal (ej: nivel de satisfacción “bajo/medio/alto”, estadio de una enfermedad “I/II/III/IV”).

1.2.2 Las variables predictoras

Conocidas indistintamente como variables independientes, explicativas, regresoras, covariables o características (features). Son las magnitudes, atributos o factores que se postula que influyen o están asociados con el comportamiento de la variable de respuesta. Al igual que la variable de respuesta, pueden ser de diversa naturaleza (continuas, categóricas, etc.). La selección de estas variables es una de las fases más críticas del modelado, requiriendo una combinación de conocimiento del dominio, análisis exploratorio de datos y técnicas estadísticas formales.

1.2.3 El término de error aleatorio

Este componente, a menudo subestimado, es conceptualmente crucial. Simboliza la variabilidad intrínseca de la variable de respuesta que no es capturada o explicada por las variables predictoras incluidas explícitamente en el modelo. El término de error \(\epsilon\) no es un simple “error” en el sentido de equivocación; es un componente estocástico que amalgama múltiples fuentes de variabilidad:

  • Variables Omitidas: Ningún modelo es perfecto. Siempre habrá factores que influyen en \(Y\) pero que no han sido medidos o incluidos en el modelo (variables latentes).
  • Error de Medición: Las mediciones de \(Y\) (y también de \(X\)) pueden no ser perfectamente precisas.
  • Aleatoriedad Intrínseca: Muchos fenómenos naturales y sociales tienen un componente de variabilidad irreducible. Dos individuos con idénticos valores en todas las variables predictoras pueden, aun así, tener valores distintos en la variable de respuesta.

Formalmente, la relación fundamental de la regresión se expresa como la descomposición de la variable de respuesta en una parte sistemática y una parte aleatoria:

\[Y = \underbrace{f(X_1, \ldots, X_k)}_{\text{Componente Sistemática}} + \underbrace{\epsilon}_{\text{Componente Aleatoria}}\]

donde \(f(\cdot)\) denota la componente sistemática (o determinística) del modelo, que representa el valor esperado de \(Y\) para unos valores dados de las \(X\). La función \(f\) es lo que intentamos estimar a partir de los datos. Por su parte, \(\epsilon\) es la componente aleatoria, y gran parte del diagnóstico y la inferencia en regresión se basa en verificar los supuestos que hacemos sobre la distribución de este término (ej: que su media es cero, que su varianza es constante, etc.).

Una característica que define a los modelos de regresión lineal (y que se extiende a muchos otros tipos de modelos) es que la función \(f(\cdot)\) mantiene una relación lineal con respecto a sus parámetros desconocidos (los coeficientes beta, \(\beta_j\)). Es crucial enfatizar que esta “linealidad en los parámetros” no impone una restricción de linealidad en las variables predictoras mismas.

Por el contrario, es común y metodológicamente válido incorporar transformaciones no lineales de los predictores o interacciones complejas entre ellos para capturar relaciones más sofisticadas. Por ejemplo, el siguiente modelo es un modelo de regresión lineal:

\[Y = \beta_0 + \beta_1 X_1 + \beta_2 X_1^2 + \beta_3 \log(X_2) + \beta_4 (X_1 \cdot X_2) + \epsilon\]

Aunque la relación entre \(Y\) y las variables \(X_1\) y \(X_2\) es claramente no lineal (es cuadrática en \(X_1\), logarítmica en \(X_2\) e incluye una interacción), el modelo es lineal en los parámetros \(\beta_0, \beta_1, \beta_2, \beta_3, \beta_4\). La función \(f\) es una combinación lineal de estos coeficientes. Esta flexibilidad es una de las razones de la enorme potencia de los modelos lineales.

El siguiente bloque de código en R genera un ejemplo visual. Simulamos datos que siguen una relación cuadrática y luego ajustamos un modelo lineal que incluye un término cuadrático (\(X^2\)). Como se puede observar en la figura, la línea de regresión (azul) captura perfectamente la curvatura de los datos, demostrando que un modelo lineal en sus parámetros puede modelar relaciones no lineales en sus variables.

# Cargar la librería necesaria para la visualización
library(ggplot2)

# 1. Simulación de datos
set.seed(42) # Para reproducibilidad
n <- 100 # Número de observaciones
x <- runif(n, -5, 5)
# La relación verdadera es cuadrática: y = 1.5 + 0.5*x + 0.8*x^2 + error
y <- 1.5 + 0.5 * x + 0.8 * x^2 + rnorm(n, mean = 0, sd = 5)
datos <- data.frame(x, y)

# 2. Ajuste del modelo lineal
# Usamos I(x^2) para indicar que tratamos x^2 como una variable
modelo_cuadratico <- lm(y ~ x + I(x^2), data = datos)

# 3. Visualización con ggplot2
ggplot(datos, aes(x = x, y = y)) +
  geom_point(alpha = 0.6, color = "gray40") + # Puntos de los datos originales
  geom_smooth(method = "lm", formula = y ~ x + I(x^2), se = FALSE, color = "#0072B2", size = 1.2) + # Línea del modelo ajustado
  labs(
    title = "Modelo Lineal con Término Cuadrático",
    x = "Variable Predictora (X)",
    y = "Variable de Respuesta (Y)"
  ) +
  theme_classic(base_size = 14)
Figura 1.1: Ejemplo de un modelo lineal en los parámetros que captura una relación no lineal (cuadrática) en los datos.

1.3 Un viaje preliminar por el universo de los modelos de regresión

La regresión lineal clásica, que será el objeto de estudio de los primeros capítulos, es el punto de partida y la piedra angular sobre la cual se erige una prolífica y fascinante gama de metodologías estadísticas avanzadas. Este volumen se dedicará a desentrañar con rigor las siguientes extensiones y especializaciones, que permiten al analista abordar una variedad casi infinita de problemas.

1.3.1 Modelos lineales (LMs)

Constituyen el paradigma fundamental, el alfabeto sobre el que se escribe el lenguaje del modelado estadístico. Son mucho más que una simple técnica para ajustar una recta a una nube de puntos; son el laboratorio donde se forjan y se comprenden los conceptos esenciales que nos acompañarán durante todo nuestro viaje. Es aquí donde aprenderemos a:

  • Estimar parámetros e interpretar su significado en el contexto del problema.
  • Cuantificar la incertidumbre de nuestras estimaciones mediante errores estándar e intervalos de confianza.
  • Realizar contrastes de hipótesis para evaluar si la relación entre nuestras variables es estadísticamente significativa o fruto del azar.
  • Diagnosticar la “salud” de un modelo, examinando si los supuestos sobre los que se construye son razonables para nuestros datos.

En su forma más clásica, el modelo lineal asume que la variable de respuesta (y, por consecuencia, el término de error aleatorio) sigue una distribución Normal o Gaussiana. Esta asunción es la clave que desbloquea todo el elegante aparato de la inferencia estadística, permitiéndonos realizar pruebas exactas y derivar propiedades matemáticas bien conocidas. Técnicas tan ubicuas en la ciencia como el Análisis de la Varianza (ANOVA) o el Análisis de la Covarianza (ANCOVA) no son más que casos particulares de la gran familia de los modelos lineales, un hecho que unifica campos de la estadística que históricamente se estudiaban por separado. Dominar los LMs es, sencillamente, un requisito indispensable.

1.3.2 Modelos lineales generalizados (GLMs)

Si los LMs son el alfabeto, los GLMs son la gramática que nos permite construir frases complejas y con significado en una variedad de contextos mucho más amplia. Introducidos en el influyente y verdaderamente revolucionario trabajo de (Nelder y Wedderburn 1972), los GLMs representan un salto conceptual que expande de forma masiva el universo de problemas que podemos abordar. Suponen una generalización elegante que nos permite escapar de la “tiranía” de la distribución Normal y modelar respuestas con una variedad mucho más amplia de naturalezas y escalas.

Esta flexibilidad se logra mediante la combinación de dos ingeniosos mecanismos que son el corazón de la teoría:

  1. La familia exponencial de distribuciones: Los GLMs no funcionan con cualquier distribución, sino con aquellas que pertenecen a una “familia” matemática con propiedades muy convenientes: la familia exponencial. Este “club” de distribuciones es muy selecto, pero incluye a miembros tan importantes como la Normal, la Poisson (para datos de conteo), la Binomial (para datos de proporciones o binarios), la Gamma (para datos continuos positivos y asimétricos) o la Binomial Negativa. Su estructura matemática común permite desarrollar una teoría unificada para la estimación de parámetros, lo que es un logro teórico de primer orden.

  2. La función de enlace (link function): Este es el verdadero golpe de genialidad. El predictor lineal de nuestro modelo, \(\boldsymbol{X\beta}\), puede tomar cualquier valor en la recta real, desde \(-\infty\) hasta \(+\infty\). Sin embargo, la media de nuestra variable de respuesta, \(E[Y] = \mu\), a menudo está restringida. Por ejemplo, una probabilidad (\(\mu\) en un modelo binomial) debe estar entre 0 y 1; un conteo (\(\mu\) en un modelo de Poisson) debe ser positivo. La función de enlace, \(g(\cdot)\), actúa como un “traductor” o un “puente” que conecta estos dos mundos. Transforma la media restringida de la respuesta para que pueda ser modelada por el predictor lineal no restringido. La relación fundamental es, por tanto, \(g(E[Y]) = g(\mu) = \boldsymbol{X\beta}\).

  • Para datos de conteo (Poisson), se usa un enlace logarítmico (\(g(\mu) = \log(\mu)\)). Esto garantiza que, al invertir la función para obtener la media (\(\mu = \exp(\boldsymbol{X\beta})\)), el resultado será siempre positivo, como debe ser un conteo.
  • Para datos binarios (Binomial), se usa un enlace logit (\(g(\mu) = \log(\frac{\mu}{1-\mu})\)). Esta función toma una probabilidad \(\mu\) en el rango (0, 1) y la proyecta sobre toda la recta real, permitiendo que sea modelada por \(\boldsymbol{X\beta}\).

Gracias a los GLMs, podemos usar el mismo marco conceptual de la regresión lineal para modelar una gama de fenómenos increíblemente diversa, desde predecir la cantidad de ciclistas en una ciudad (Poisson) hasta la probabilidad de que un paciente responda a un tratamiento (logística).

1.3.3 Modelos de efectos mixtos (Mixed Models)

Su desarrollo responde a la necesidad crítica de analizar datos que exhiben estructuras de dependencia o correlación, como agrupamientos, anidamientos o jerarquías. En datos estándar, asumimos que las observaciones son independientes, pero esta asunción se viola en casos como: * Medidas repetidas sobre los mismos sujetos (ej: medir la presión arterial de un paciente cada mes). * Datos longitudinales (un tipo de medida repetida a lo largo del tiempo). * Datos agrupados (ej: estudiantes anidados dentro de clases, que a su vez están anidadas dentro de colegios). Estos modelos, detallados en obras como la de (Pinheiro y Bates 2000), introducen explícitamente una estructura de correlación en el término de error mediante la incorporación de efectos aleatorios, que permiten capturar la variabilidad entre los diferentes grupos o individuos, además de los efectos fijos que representan a la población general.

1.3.4 Modelos aditivos generalizados (GAMs)

Representan una extensión natural y altamente flexible de los GLMs que relaja el supuesto de linealidad entre el predictor transformado y las covariables. Los GAMs, cuya implementación moderna se debe en gran parte al trabajo de (Wood 2017), permiten modelar estas relaciones mediante funciones suaves no paramétricas (como splines), manteniendo al mismo tiempo la estructura aditiva del modelo. La forma general es \(g(\mu) = \alpha + f_1(x_1) + f_2(x_2) + \ldots + f_p(x_p)\), donde las \(f_i(\cdot)\) son funciones suaves de los predictores estimadas a partir de los datos. Esto permite capturar patrones no lineales complejos sin necesidad de especificar una forma funcional paramétrica a priori, logrando un equilibrio excepcional entre flexibilidad e interpretabilidad.

Este compendio no es un texto puramente teórico. Fusiona intrínsecamente la exposición de los conceptos con su aplicación computacional directa a través del lenguaje y entorno estadístico R. R se ha consolidado como el estándar de facto en la investigación estadística y la ciencia de datos académica por su potencia, flexibilidad y el inmenso ecosistema de paquetes contribuidos por la comunidad científica. Se presupone en el lector una familiaridad operativa básica con R, y se fomenta activamente el desarrollo de una fluidez progresiva mediante la reproducción, modificación y experimentación con los numerosos ejemplos y fragmentos de código presentados.

La capacidad de ejecutar análisis en R es fundamental para todo el ciclo de vida del modelado:

  • La exploración de datos y la visualización inicial.
  • La estimación de parámetros y el ajuste de los modelos.
  • El diagnóstico riguroso de la adecuación del modelo y la validación de sus supuestos.
  • La producción de gráficos y tablas de alta calidad para comunicar los resultados.

En R, las herramientas fundamentales para la regresión lineal (lm()) y los modelos lineales generalizados (glm()) están incluidas en el paquete stats, que es uno de los paquetes base y se carga automáticamente con cada sesión. Por lo tanto, no necesitamos instalarlo ni cargarlo.

A lo largo del libro, extenderemos esta funcionalidad base con paquetes especializados que sí requieren instalación y carga. Entre los más importantes que usaremos se encuentran:

  • mgcv: La implementación de referencia para GAMs, mantenida por su creador, Simon Wood, y citada en (Wood 2017).
  • lme4 y nlme: Los dos paquetes fundamentales para el ajuste de modelos de efectos mixtos, desarrollados por los pioneros en el campo (Pinheiro y Bates 2000; Bates et al. 2015).
  • rms: Un paquete y una filosofía de trabajo para implementar estrategias de modelado de regresión robustas, como se detalla en la obra de (Harrell 2015).
  • gamair: Contiene numerosos conjuntos de datos que acompañan al libro de (Wood 2017), ideales para practicar con GAMs.

1.4 Una breve crónica del desarrollo de la regresión

1.4.1 Los orígenes: Galton y la “regresión a la mediocridad”

La gestación de la metodología de regresión se traza hasta las investigaciones pioneras de Sir Francis Galton, un polímata de la era victoriana. A finales del siglo XIX, estudiando la herencia de la estatura, Galton recopiló datos de padres e hijos y notó un fenómeno curioso: los padres muy altos tendían a tener hijos altos, pero, en promedio, no tan altos como ellos. Análogamente, los padres muy bajos tenían hijos bajos, pero no tan bajos como ellos. Acuñó el término “regresión a la mediocridad” (hoy diríamos “regresión a la media”) para describir esta tendencia de las características de la descendencia a “regresar” hacia la media de la población, en lugar de perpetuar los extremos de los progenitores (Galton 1886).

Datos recopilados

  • Galton recopiló datos sobre las estaturas de 928 hijos y sus respectivos padres.
  • Las medidas fueron expresadas en pulgadas (1 pulgada = 2.54 cm).
  • En sus análisis, utilizó el promedio de las estaturas de ambos padres, conocido como estatura media parental, para compararlo con la estatura de los hijos.

Principales hallazgos

  1. Relación lineal entre padres e hijos:
    Galton observó que existe una relación positiva entre la estatura de los padres y la de los hijos. Los padres altos tienden a tener hijos altos, y los padres bajos tienden a tener hijos bajos. Esta relación puede modelarse con una línea recta, lo que inspiró la formulación de la regresión lineal.

  2. Regresión a la media:

    • Aunque los hijos de padres altos son, en promedio, más altos que el promedio general de la población, también tienden a ser menos altos que sus padres.
    • De manera similar, los hijos de padres bajos son más bajos que el promedio general, pero suelen ser menos bajos que sus padres.
    • Este fenómeno, que Galton llamó “regresión a la media”, ocurre porque las características extremas tienden a suavizarse en la siguiente generación debido a la influencia de múltiples factores genéticos y ambientales.

  3. Ecuación de la recta de regresión:
    Galton ajustó una recta para describir la relación entre la estatura media parental (\(X\)) y la estatura de los hijos (\(Y\)): \[ Y = \beta_0 + \beta_1 X \] Donde:

    • \(\beta_0\): Intercepto, representa la estatura promedio de los hijos cuando la estatura parental es promedio.
    • \(\beta_1\): Pendiente, indica cómo cambia la estatura de los hijos por cada unidad de cambio en la estatura media parental.

Importancia en la Estadística

  1. Regresión lineal:
    Este estudio introdujo el concepto de recta de regresión, que describe cómo varía la media de una variable dependiente en función de una variable independiente.

  2. Correlación:
    Galton también estudió el grado de relación entre variables, precursor del concepto de coeficiente de correlación desarrollado posteriormente por Karl Pearson, un discípulo suyo.

  3. Regresión a la media:
    El término y la idea detrás de “regresión a la media” surgieron de estos estudios y son hoy fundamentales en estadística y genética.

Ejemplo Gráfico

Galton representó sus datos en gráficos de dispersión, mostrando cómo los puntos (pares de estatura media parental y estatura de los hijos) se agrupan alrededor de la recta de regresión, ilustrando la tendencia general de la relación.

# Cargar los paquetes necesarios
library(ggplot2)
library(HistData)

# Cargar los datos de Galton
data("GaltonFamilies")

# Crear el modelo de regresión lineal para obtener los coeficientes
modelo <- lm(childHeight ~ midparentHeight, data = GaltonFamilies)

# Crear la etiqueta para la ecuación de la recta de forma más limpia
# Usamos sprintf() para un formato más controlado y legible
eq_label <- sprintf("y = %.2f + %.2f * x", coef(modelo)[1], coef(modelo)[2])

# --- Gráfico Mejorado ---
# Usamos un tema más limpio y colores más suaves para una apariencia profesional.
# geom_jitter() es mejor que geom_point() para estos datos, ya que evita la superposición de puntos.
ggplot(GaltonFamilies, aes(x = midparentHeight, y = childHeight)) +
  
  # 1. Puntos de datos: Usamos geom_jitter para visualizar mejor los puntos superpuestos
  #    y añadimos transparencia (alpha) para ver la densidad.
  geom_jitter(alpha = 0.3, color = "gray50", width = 0.1, height = 0.1) +
  
  # 2. Línea de regresión: En un color azul profesional y más gruesa para que destaque.
  geom_smooth(method = "lm", se = FALSE, color = "#0072B2", size = 1.2) +
  
  # 3. Anotación: Añadimos la ecuación de la recta de forma elegante,
  #    usando el mismo color que la línea para crear cohesión visual.
  annotate(
    "text",
    x = 66, y = 74, # Posición ajustada para mejor visibilidad
    label = eq_label,
    color = "#0072B2", # Mismo color que la línea
    size = 4.5, # Tamaño de la fuente
    fontface = "italic" # Cursiva para la ecuación
  ) +
  
  # 4. Títulos y etiquetas: Mejorados para mayor claridad y contexto.
  #    Añadimos un subtítulo y una fuente.
  labs(
    title = "Regresión de la Estatura de Hijos vs. Padres",
    x = "Promedio de Estatura de los Padres (pulgadas)",
    y = "Estatura del Hijo/a (pulgadas)",
    caption = "Fuente: Paquete HistData de R"
  ) +
  
  # 5. Tema: Usamos un tema limpio y profesional como base.
  theme_classic(base_size = 14)
`geom_smooth()` using formula = 'y ~ x'

Datos históricos del estudio sobre la ‘regresión a la media’.

1.4.2 La formalización matemática: Legendre y Gauss

Aunque Galton sentó las bases conceptuales e introdujo el término, la formalización matemática de la estimación de parámetros en modelos lineales se atribuye a dos de los más grandes matemáticos de la historia. Adrien-Marie Legendre publicó en 1805 el “Método de los mínimos cuadrados” como un procedimiento numérico para ajustar observaciones astronómicas. Pocos años después, Carl Friedrich Gauss no solo publicó que había desarrollado el mismo método de forma independiente años antes, sino que lo dotó de una profundidad teórica mucho mayor, conectándolo con la teoría de la probabilidad y derivándolo bajo el supuesto de errores distribuidos normalmente, convirtiéndolo en la técnica fundamental para la estimación en modelos lineales que sigue siendo hoy.

1.4.3 El desarrollo moderno: la revolución de los GLMs

A lo largo del siglo XX, la regresión experimentó un desarrollo explosivo. Sin embargo, el hito que probablemente más ha influido en la práctica estadística moderna fue la publicación del artículo sobre Modelos Lineales Generalizados (GLMs) por John Nelder y Robert Wedderburn en 1972 (Nelder y Wedderburn 1972). Esta obra seminal fue revolucionaria porque unificó bajo un mismo paraguas conceptual y computacional diversas clases de modelos que hasta entonces se trataban por separado: la regresión lineal para datos normales, la regresión logística para datos binarios y la regresión de Poisson para datos de conteo. Esto estimuló enormemente el desarrollo de software y la aplicación del modelado estadístico a una nueva y vasta gama de problemas.

1.4.4 La evolución contemporánea

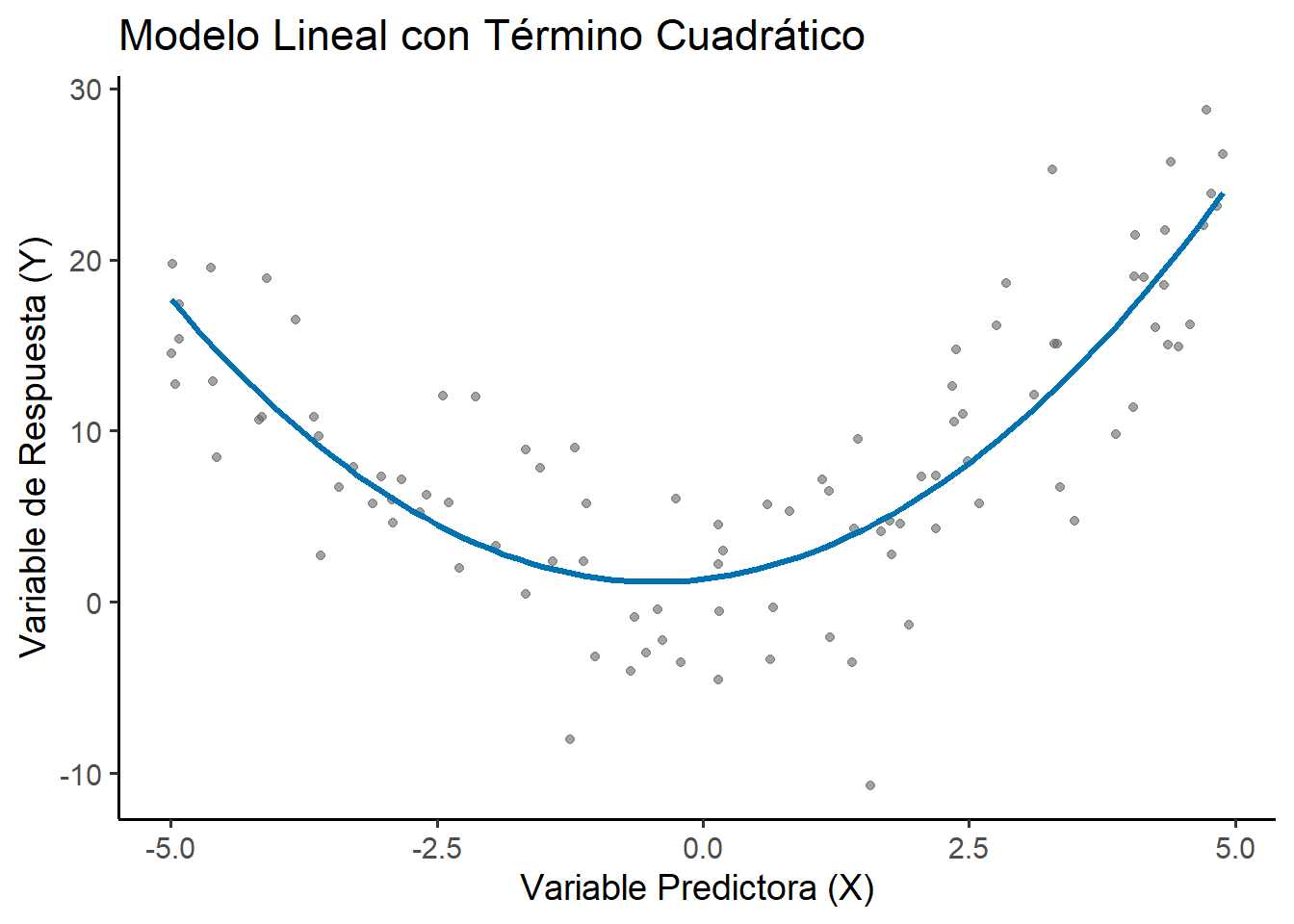
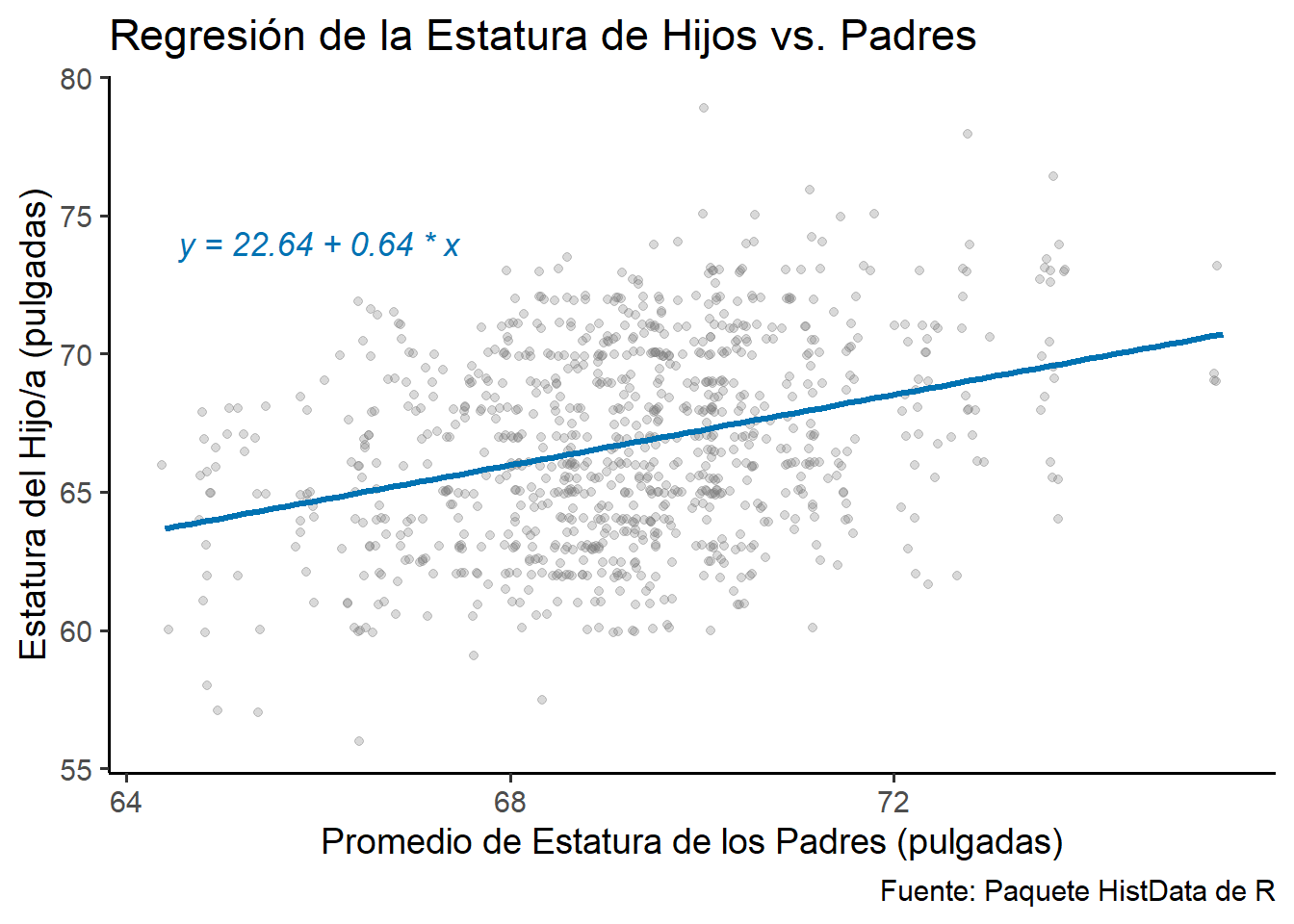
Este legado continúa evolucionando a un ritmo vertiginoso, con la inclusión de modelos jerárquicos y bayesianos, métodos no paramétricos y de machine learning como los árboles de regresión, y la adaptación de la regresión al análisis de datos masivos (big data). La regresión ha evolucionado desde una observación sobre la herencia biológica hasta convertirse en una de las herramientas más versátiles y poderosas del arsenal analítico moderno.