3 El modelo de regresión lineal múltiple

El modelo de regresión lineal múltiple constituye la extensión natural y más potente del modelo simple que estudiamos en el capítulo anterior. Mientras que la regresión simple nos permitía examinar la relación entre una variable respuesta y un único predictor, la regresión múltiple nos capacita para modelar simultáneamente el efecto de múltiples variables predictoras, una situación mucho más realista en la mayoría de aplicaciones prácticas (Kutner et al. 2005; James et al. 2021; Fox y Weisberg 2018).

En este capítulo profundizaremos en los aspectos únicos de la regresión múltiple que no están presentes en el caso simple: la interpretación de coeficientes en presencia de otros predictores, el diagnóstico específico del modelo múltiple, y el problema crucial de la multicolinealidad. Estos conceptos son fundamentales para desarrollar modelos predictivos robustos y interpretables (Harrell 2015; Draper 1998).

Objetivos de aprendizaje

Al finalizar este capítulo, serás capaz de:

Formular y estimar modelos de regresión lineal múltiple, comprendiendo las diferencias clave respecto al caso simple.
Interpretar coeficientes en el contexto multivariante, entendiendo el concepto de ceteris paribus (“manteniendo las demás variables constantes”).
Realizar inferencia estadística construyendo intervalos de confianza y contrastes de hipótesis para los parámetros del modelo múltiple.
Evaluar la calidad del ajuste usando medidas como \(R^2\), \(R^2\) ajustado y la descomposición ANOVA.
Diagnosticar el modelo múltiple, aplicando técnicas específicas como gráficos CPR y gráficos de regresión parcial.
Identificar y tratar la multicolinealidad, comprendiendo sus causas, consecuencias y usando el VIF como herramienta de diagnóstico.
Realizar predicciones con el modelo ajustado, distinguiendo entre intervalos de confianza e intervalos de predicción.

3.1 Formulación teórica del modelo

El paso de la regresión simple a la múltiple es más que una simple adición de términos; es un salto conceptual. Nos permite construir modelos que reflejan mejor la complejidad del mundo real, donde los resultados raramente dependen de una única causa. Al controlar simultáneamente por varios factores, podemos aislar con mayor precisión el efecto de una variable de interés, reduciendo el riesgo de llegar a conclusiones sesgadas por variables omitidas.

3.1.1 El modelo poblacional

Para \(n\) observaciones y \(p\) variables predictoras, el modelo poblacional postula que la relación verdadera entre la variable respuesta \(Y\) y los predictores \(X_1, X_2, \ldots, X_p\) sigue una relación lineal:

\[Y_i = \beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2} + \cdots + \beta_p X_{ip} + \varepsilon_i, \quad i = 1,\dots,n\]

Donde \(Y_i\) es la \(i\)-ésima variable respuesta aleatoria, \(X_{ij}\) es la \(i\)-ésima variable predictora aleatoria del \(j\)-ésimo predictor, y \(\varepsilon_i\) es el término de error aleatorio. Los parámetros \(\beta_0, \beta_1, \ldots, \beta_p\) son los coeficientes poblacionales verdaderos pero desconocidos.

3.1.2 El modelo muestral

En la práctica, trabajamos con datos observados y estimamos el modelo usando la muestra disponible:

\[\hat{y}_i = \hat{\beta}_0 + \hat{\beta}_1 x_{i1} + \hat{\beta}_2 x_{i2} + \cdots + \hat{\beta}_p x_{ip}, \quad i = 1,\dots,n\]

Donde \(\hat{y}_i\) es la \(i\)-ésima predicción, \(x_{ij}\) es la \(i\)-ésima observación del \(j\)-ésimo predictor, y \(\hat{\beta}_j\) son los coeficientes estimados. El coeficiente \(\hat{\beta}_j\) representa el cambio estimado en la media de \(Y\) ante un cambio de una unidad en el predictor \(X_j\), manteniendo constantes todas las demás variables predictoras del modelo. Este principio, conocido como ceteris paribus (del latín, “lo demás constante”), es la piedra angular de la interpretación en regresión múltiple.

3.1.3 Notación matricial

La notación matricial es fundamental para el desarrollo teórico y computacional. Nos permite expresar el sistema de \(n\) ecuaciones de forma compacta y elegante.

Modelo poblacional: \[\mathbf{Y} = \tilde{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon}\]

donde:

\[\mathbf{Y} = \begin{bmatrix} Y_1 \\ Y_2 \\ \vdots \\ Y_n \end{bmatrix}, \quad \tilde{X} = \begin{bmatrix} 1 & X_{11} & X_{12} & \cdots & X_{1p} \\ 1 & X_{21} & X_{22} & \cdots & X_{2p} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & X_{n1} & X_{n2} & \cdots & X_{np} \end{bmatrix}, \quad \boldsymbol{\beta} = \begin{bmatrix} \beta_0 \\ \beta_1 \\ \vdots \\ \beta_p \end{bmatrix}, \quad \boldsymbol{\varepsilon} = \begin{bmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \vdots \\ \varepsilon_n \end{bmatrix}\]

Donde \(\tilde{X}\) contiene variables aleatorias (denotadas con mayúsculas \(X_{ij}\)).

Modelo muestral: \[\hat{\mathbf{y}} = \mathbf{X}\hat{\boldsymbol{\beta}}\]

donde:

\[\hat{\mathbf{y}} = \begin{bmatrix} \hat{y}_1 \\ \hat{y}_2 \\ \vdots \\ \hat{y}_n \end{bmatrix}, \quad \mathbf{X} = \begin{bmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1p} \\ 1 & x_{21} & x_{22} & \cdots & x_{2p} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & x_{n2} & \cdots & x_{np} \end{bmatrix}, \quad \hat{\boldsymbol{\beta}} = \begin{bmatrix} \hat{\beta}_0 \\ \hat{\beta}_1 \\ \vdots \\ \hat{\beta}_p \end{bmatrix}\]

Donde \(\mathbf{X}\) contiene datos observados (denotados con minúsculas \(x_{ij}\)).

La matriz \(\mathbf{X}\) (datos observados) y \(\tilde{X}\) (variables aleatorias), ambas de dimensión \(n \times (p+1)\), se denominan matriz de diseño y contienen toda la información de los predictores. La primera columna de unos corresponde al término del intercepto \(\beta_0\).

3.1.4 Supuestos del modelo lineal múltiple

Para que nuestros estimadores tengan propiedades deseables (como ser insesgados y eficientes), el modelo debe cumplir una serie de supuestos sobre el comportamiento del término de error, conocidos como las condiciones de Gauss-Markov (Kutner et al. 2005; Weisberg 2005).

Linealidad en los parámetros: El valor esperado de la respuesta es una función lineal de los parámetros \(\boldsymbol{\beta}\). El modelo \(E[\mathbf{Y}|\tilde{X}] = \tilde{X}\boldsymbol{\beta}\) está bien especificado.
Exogeneidad (media del error nula): Los errores tienen una media de cero para cualquier valor de los predictores, \(E[\boldsymbol{\varepsilon}|\tilde{X}] = \mathbf{0}\). Esto implica que los predictores no contienen información sobre el término de error.
Homocedasticidad e independencia: Los errores no están correlacionados entre sí y tienen una varianza constante \(\sigma^2\) para cualquier valor de los predictores. En notación matricial: \(\text{Var}(\boldsymbol{\varepsilon}|\tilde{X}) = \sigma^2\mathbf{I}_n\).
Ausencia de multicolinealidad perfecta: Ningún predictor es una combinación lineal exacta de los otros. Esto asegura que la matriz \(\mathbf{X}\) tiene rango completo \((p+1)\), lo cual es necesario para poder estimar de forma única todos los coeficientes.
Normalidad de los errores (para inferencia): Para poder realizar contrastes de hipótesis e intervalos de confianza, se añade el supuesto de que los errores siguen una distribución Normal: \(\boldsymbol{\varepsilon} \sim N(\mathbf{0}, \sigma^2\mathbf{I}_n)\).

3.2 Estimación de los parámetros

Una vez definido el modelo y sus supuestos, el siguiente paso es estimar los parámetros desconocidos del vector \(\boldsymbol{\beta}\). El método más extendido es el de Mínimos Cuadrados Ordinarios.

3.2.1 El principio de mínimos cuadrados y la función objetivo

La idea de “mejor ajuste” se traduce matemáticamente en minimizar la discrepancia entre los valores observados \(\mathbf{y}\) (datos muestrales) y los valores predichos por el modelo, \(\hat{\mathbf{y}} = \mathbf{X}\hat{\boldsymbol{\beta}}\). Esta discrepancia se captura a través de los residuos, \(\mathbf{e} = \mathbf{y} - \hat{\mathbf{y}}\).

MCO no minimiza simplemente los residuos (ya que residuos positivos y negativos se cancelarían), sino la Suma de los Cuadrados de los Residuos (SCR o SSR en inglés). Al elevarlos al cuadrado, nos aseguramos de que todos los errores contribuyan positivamente y, además, penalizamos más fuertemente los errores grandes.

La función objetivo a minimizar, \(S(\boldsymbol{\beta})\), usando datos observados es:

\[S(\boldsymbol{\beta}) = \sum_{i=1}^n e_i^2 = \mathbf{e}^T\mathbf{e} = (\mathbf{y} - \mathbf{X}\boldsymbol{\beta})^T(\mathbf{y} - \mathbf{X}\boldsymbol{\beta})\]

3.2.2 Derivación de las ecuaciones normales

Para encontrar el vector \(\hat{\boldsymbol{\beta}}\) que minimiza esta función, utilizamos cálculo diferencial. Primero, expandimos la expresión cuadrática de \(S(\boldsymbol{\beta})\):

\[S(\boldsymbol{\beta}) = (\mathbf{y}^T - \boldsymbol{\beta}^T\mathbf{X}^T)(\mathbf{y} - \mathbf{X}\boldsymbol{\beta})\] \[S(\boldsymbol{\beta}) = \mathbf{y}^T\mathbf{y} - \mathbf{y}^T\mathbf{X}\boldsymbol{\beta} - \boldsymbol{\beta}^T\mathbf{X}^T\mathbf{y} + \boldsymbol{\beta}^T\mathbf{X}^T\mathbf{X}\boldsymbol{\beta}\]

Un punto clave aquí es notar que \(\boldsymbol{\beta}^T\mathbf{X}^T\mathbf{y}\) es un escalar (una matriz \(1 \times 1\)), por lo que es igual a su transpuesta: \(\boldsymbol{\beta}^T\mathbf{X}^T\mathbf{y} = \mathbf{y}^T\mathbf{X}\boldsymbol{\beta}\). \(1 \times 1\)). Por lo tanto, es igual a su propia transpuesta: \((\boldsymbol{\beta}^T\mathbf{X}^T\mathbf{y})^T = \mathbf{y}^T\mathbf{X}\boldsymbol{\beta}\). Esto nos permite simplificar la expresión:

\[S(\boldsymbol{\beta}) = \mathbf{y}^T\mathbf{y} - 2\boldsymbol{\beta}^T\mathbf{X}^T\mathbf{y} + \boldsymbol{\beta}^T(\mathbf{X}^T\mathbf{X})\boldsymbol{\beta}\]

Ahora, derivamos esta función con respecto al vector \(\boldsymbol{\beta}\) e igualamos el resultado a un vector de ceros para encontrar el mínimo. Usando las reglas de la derivación matricial:

La derivada de \(\mathbf{y}^T\mathbf{y}\) respecto a \(\boldsymbol{\beta}\) es \(\mathbf{0}\).
La derivada de \(2\boldsymbol{\beta}^T\mathbf{X}^T\mathbf{y}\) respecto a \(\boldsymbol{\beta}\) es \(2\mathbf{X}^T\mathbf{y}\).
La derivada de la forma cuadrática \(\boldsymbol{\beta}^T(\mathbf{X}^T\mathbf{X})\boldsymbol{\beta}\) respecto a \(\boldsymbol{\beta}\) es \(2(\mathbf{X}^T\mathbf{X})\boldsymbol{\beta}\).

Aplicando estas reglas, obtenemos el gradiente de la función de pérdida:

\[\frac{\partial S(\boldsymbol{\beta})}{\partial \boldsymbol{\beta}} = -2\mathbf{X}^T\mathbf{y} + 2(\mathbf{X}^T\mathbf{X})\boldsymbol{\beta}\]

Igualando a cero y sustituyendo \(\boldsymbol{\beta}\) por el estimador \(\hat{\boldsymbol{\beta}}\) que cumple esta condición:

\[-2\mathbf{X}^T\mathbf{y} + 2(\mathbf{X}^T\mathbf{X})\hat{\boldsymbol{\beta}} = \mathbf{0}\]

Simplificando, llegamos al célebre sistema de \(p+1\) ecuaciones conocido como las Ecuaciones Normales:

\[(\mathbf{X}^T\mathbf{X})\hat{\boldsymbol{\beta}} = \mathbf{X}^T\mathbf{y}\]

3.2.3 La solución MCO y la condición de invertibilidad

Para resolver este sistema y despejar \(\hat{\boldsymbol{\beta}}\), necesitamos multiplicar por la inversa de la matriz \((\mathbf{X}^T\mathbf{X})\). Esta inversa existe si y solo si la matriz es invertible, lo que está directamente garantizado por el supuesto de ausencia de multicolinealidad perfecta.

Si el rango de la matriz de diseño \(\mathbf{X}\) es \(p+1\) (sus columnas son linealmente independientes), entonces la matriz \(\mathbf{X}^T\mathbf{X}\) (de dimensión \((p+1) \times (p+1)\)) será de rango completo, simétrica y definida positiva, y por tanto, invertible.

La solución única para el vector de estimadores MCO es:

\[\hat{\boldsymbol{\beta}} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}\]

Esta compacta y poderosa ecuación es la base de la estimación en regresión lineal y es implementada por todo el software estadístico.

Claro, aquí tienes el texto completo en formato Markdown y con las fórmulas clave sin los recuadros.

3.2.4 Propiedades de los estimadores de MCO

Una vez que hemos obtenido la fórmula para calcular nuestros coeficientes, \(\hat{\boldsymbol{\beta}} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}\), la pregunta fundamental es: ¿qué tan buenos son estos estimadores? La teoría estadística nos proporciona una respuesta contundente a través de sus propiedades en el muestreo, que son la base para toda la inferencia estadística posterior.

El Teorema de Gauss-Markov es el resultado central. Afirma que, si se cumplen los supuestos del modelo lineal clásico (1-4), los estimadores de Mínimos Cuadrados Ordinarios son los Mejores Estimadores Lineales Insesgados (MELI o BLUE). Desglosemos esto:

Lineal: \(\hat{\boldsymbol{\beta}}\) es una combinación lineal de la variable respuesta \(\mathbf{y}\).
Insesgado (Unbiased): En promedio, a lo largo de infinitas muestras, nuestro estimador acertará al verdadero valor poblacional \(\boldsymbol{\beta}\). No tiene un sesgo sistemático. La demostración formal es directa: \[\begin{align} E[\hat{\boldsymbol{\beta}}] &= E[(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}] \nonumber \\ &= E[(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T(\mathbf{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon})] \nonumber \\ &= (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{X}\boldsymbol{\beta} + (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T E[\boldsymbol{\varepsilon}] \nonumber \\ &= \boldsymbol{I}\boldsymbol{\beta} + \mathbf{0} = \boldsymbol{\beta} \nonumber \end{align}\]
Mejor (Best): “Mejor” significa que tiene la mínima varianza posible dentro de la clase de todos los estimadores lineales e insesgados. No existe otro estimador de este tipo que sea más preciso. La precisión de nuestros estimadores se captura en su matriz de varianzas-covarianzas: \[\begin{align} \text{Var}(\hat{\boldsymbol{\beta}}) &= \text{Var}[(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}] \nonumber \\ &= (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T \, \text{Var}(\mathbf{y}) \, [(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T]^T \nonumber \\ &= (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T \, (\sigma^2 \mathbf{I}_n) \, \mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1} \nonumber \\ &= \sigma^2 (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1} \nonumber \\ &= \sigma^2 (\mathbf{X}^T\mathbf{X})^{-1} \nonumber \end{align}\] Por tanto, la matriz que define la incertidumbre de nuestro estimador es: \[\text{Var}(\hat{\boldsymbol{\beta}}) = \sigma^2(\mathbf{X}^T\mathbf{X})^{-1}\] Los elementos de la diagonal de esta matriz nos dan la varianza de cada coeficiente individual, \(Var(\hat{\beta}_j)\), mientras que los elementos fuera de la diagonal nos dan la covarianza entre pares de coeficientes, \(Cov(\hat{\beta}_j, \hat{\beta}_k)\).

Finalmente, si añadimos el supuesto de normalidad de los errores (\(\varepsilon_i \sim N(0, \sigma^2)\)), las propiedades del estimador se completan. Dado que \(\hat{\boldsymbol{\beta}}\) es una combinación lineal de \(\mathbf{y}\) (que ahora es normal), el propio estimador seguirá una distribución normal: \[\hat{\boldsymbol{\beta}} \sim N\left(\boldsymbol{\beta}, \sigma^2(\mathbf{X}^T\mathbf{X})^{-1}\right)\]Esto implica que cada coeficiente individual también se distribuye normalmente:\[\hat{\beta}_j \sim N\left(\beta_j, \sigma^2 [(\mathbf{X}^T\mathbf{X})^{-1}]_{jj}\right)\] donde \([(\mathbf{X}^T\mathbf{X})^{-1}]_{jj}\) es el j-ésimo elemento de la diagonal de la matriz inversa. Este resultado es la puerta de entrada a la inferencia, permitiéndonos construir intervalos de confianza y realizar contrastes de hipótesis (como los test-t).

3.2.5 Estimación de la varianza del error

La matriz de varianzas-covarianzas de \(\hat{\boldsymbol{\beta}}\) depende de \(\sigma^2\), la varianza de los errores poblacionales, que es desconocida. Por lo tanto, el siguiente paso lógico es encontrar un buen estimador para ella a partir de nuestros datos.

El punto de partida natural son los residuos del modelo, \(\mathbf{e} = \mathbf{y} - \hat{\mathbf{y}}\), que son la contraparte muestral de los errores teóricos \(\boldsymbol{\varepsilon}\). La suma de los cuadrados de los residuos (SSE) es la base de nuestro estimador:

\[SSE = \mathbf{e}^T\mathbf{e} = \mathbf{y}^T(\mathbf{I}_n - \mathbf{H})^T(\mathbf{I}_n - \mathbf{H})\mathbf{y} = \mathbf{y}^T(\mathbf{I}_n - \mathbf{H})\mathbf{y}\] (usando las propiedades de simetría e idempotencia de la matriz de proyección \(\mathbf{H}\)).

Para encontrar un estimador insesgado, calculamos el valor esperado de la SSE. Utilizando el lema \(E[\mathbf{z}^T\mathbf{A}\mathbf{z}] = \text{traza}(\mathbf{A}\boldsymbol{\Sigma}) + \boldsymbol{\mu}^T\mathbf{A}\boldsymbol{\mu}\) con \(\mathbf{z} = \mathbf{y}\), \(\mathbf{A} = \mathbf{I}_n - \mathbf{H}\), \(\boldsymbol{\mu} = \mathbf{X}\boldsymbol{\beta}\) y \(\boldsymbol{\Sigma} = \sigma^2\mathbf{I}_n\): \[\begin{align} E[SSE] &= \text{traza}[(\mathbf{I}_n - \mathbf{H})\sigma^2\mathbf{I}_n] + \boldsymbol{\beta}^T\mathbf{X}^T(\mathbf{I}_n - \mathbf{H})\mathbf{X}\boldsymbol{\beta} \nonumber \end{align}\] El segundo término se anula porque \((\mathbf{I}_n - \mathbf{H})\mathbf{X} = \mathbf{X} - \mathbf{H}\mathbf{X} = \mathbf{X} - \mathbf{X} = \mathbf{0}\). Nos queda: \[\begin{align} E[SSE] &= \sigma^2 \text{traza}(\mathbf{I}_n - \mathbf{H}) \nonumber \\ &= \sigma^2 (\text{traza}(\mathbf{I}_n) - \text{traza}(\mathbf{H})) \nonumber \\ &= \sigma^2 (n - (p + 1)) \nonumber \end{align}\] El valor esperado de la SSE no es \(\sigma^2\), sino un múltiplo de ella. Esto nos lleva directamente a un estimador insesgado para \(\sigma^2\) dividiendo la SSE por sus grados de libertad, \(n - p - 1\): \[\hat{\sigma}^2 = s^2 = \frac{SSE}{n - p - 1} = \frac{\mathbf{e}^T\mathbf{e}}{n - p - 1}\] Intuitivamente, perdemos un grado de libertad por cada parámetro que hemos estimado en el modelo (los \(p\) coeficientes de las pendientes y el intercepto). La raíz cuadrada de este valor, \(\hat{\sigma}\), se conoce como el Error Estándar de la Regresión y representa la magnitud de un error de predicción típico.

Con este estimador, podemos calcular el error estándar de cada coeficiente, que mide la incertidumbre de nuestra estimación para \(\beta_j\): \[\text{se}(\hat{\beta}_j) = \sqrt{\hat{\sigma}^2 [(\mathbf{X}^T\mathbf{X})^{-1}]_{jj}}\] Bajo normalidad, se puede demostrar además que la cantidad \(\frac{SSE}{\sigma^2}\) sigue una distribución Chi-cuadrado con \(n-p-1\) grados de libertad, un resultado clave para la inferencia formal.

Ejemplo: Estimación de un modelo múltiple

Para ilustrar estos conceptos, usemos un ejemplo con datos de precios de viviendas. Supongamos que queremos predecir el precio de una vivienda basándonos en su superficie, número de habitaciones, antigüedad, distancia al centro y si tiene garaje.


Call:
lm(formula = precio ~ superficie + habitaciones + antiguedad + 
    distancia_centro + garaje, data = viviendas)

Residuals:
   Min     1Q Median     3Q    Max 
-38847 -11074    867   9898  38486 

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)    
(Intercept)      53750.97    6666.71   8.063 7.53e-14 ***
superficie        1171.78      47.28  24.783  < 2e-16 ***
habitaciones     15072.31    1303.42  11.564  < 2e-16 ***
antiguedad        -744.59      75.42  -9.872  < 2e-16 ***
distancia_centro -2028.27     164.88 -12.302  < 2e-16 ***
garajeSí         25829.43    2349.44  10.994  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 15950 on 194 degrees of freedom
Multiple R-squared:  0.9094,    Adjusted R-squared:  0.9071 
F-statistic: 389.4 on 5 and 194 DF,  p-value: < 2.2e-16

Este output nos muestra:

Coeficientes estimados (\(\hat{\boldsymbol{\beta}}\)) y sus errores estándar
Estadísticos t y p-valores para cada coeficiente
Error estándar residual (\(\hat{\sigma}\) = 1.5952^{4} euros)
R² múltiple (0.9094) - proporción de varianza explicada
Estadístico F global para contrastar la significancia del modelo

3.3 La interpretación de los coeficientes

Estimar los coeficientes y sus errores estándar es solo la mitad del trabajo. La otra mitad, y a menudo la más importante, es interpretarlos correctamente.

El concepto fundamental en regresión múltiple es el de ceteris paribus (“lo demás constante”). Cada coeficiente \(\beta_j\) representa el cambio esperado en \(Y\) por un cambio de una unidad en \(X_j\), manteniendo todas las demás variables predictoras del modelo fijas. Es el efecto “puro” o “aislado” de \(X_j\) sobre \(Y\), después de haber controlado por la influencia de las otras variables incluidas en el modelo. Matemáticamente, es la derivada parcial del valor esperado de \(Y\) con respecto a \(X_j\): \[\beta_j = \frac{\partial E[Y|\tilde{X}]}{\partial X_j}\]

Esta interpretación es crucialmente diferente de la que se obtiene en una regresión simple. El coeficiente de una regresión simple de \(Y\) sobre \(X_j\) captura no solo el efecto directo de \(X_j\), sino también los efectos indirectos de cualquier otra variable omitida que esté correlacionada tanto con \(Y\) como con \(X_j\). Por ello, el valor de \(\hat{\beta}_j\) en una regresión múltiple casi nunca es igual al de una regresión simple.

La forma más precisa de entender \(\hat{\beta}_j\) es a través del concepto de regresión parcial. El coeficiente \(\hat{\beta}_j\) de la regresión múltiple es idéntico al coeficiente de una regresión simple entre dos conjuntos de residuos:

Los residuos de una regresión de \(\mathbf{y}\) sobre todas las demás variables predictoras (excepto \(X_j\)).
Los residuos de una regresión de \(\mathbf{x_j}\) sobre todas las demás variables predictoras.

En otras palabras, \(\hat{\beta}_j\) mide la relación entre la parte de \(Y\) que no puede ser explicada por las otras variables y la parte de \(X_j\) que tampoco puede ser explicada por las otras variables. Es la asociación entre \(Y\) y \(X_j\) después de haber “limpiado” o “netado” la influencia de todos los demás predictores de ambas. Este concepto se visualiza en los gráficos de regresión parcial (o added-variable plots), que son una herramienta de diagnóstico fundamental.

Interpretación práctica de los coeficientes

Volviendo a nuestro ejemplo de viviendas, interpretemos cada coeficiente aplicando el principio ceteris paribus:

Superficie (1172 €/m²): Por cada metro cuadrado adicional, el precio aumenta en promedio 1172 euros, manteniendo constantes el número de habitaciones, antigüedad, distancia al centro y presencia de garaje.
Habitaciones (1.5072^{4} €): Cada habitación adicional incrementa el precio en 1.5072^{4} euros en promedio, controlando por la superficie y demás variables.
Antigüedad (-745 €/año): Por cada año de antigüedad, el precio disminuye en 745 euros en promedio, ceteris paribus.
Distancia al centro (-2028 €/km): Cada kilómetro adicional de distancia reduce el precio en 2028 euros en promedio, manteniendo todo lo demás constante.
Garaje (2.5829^{4} €): Las viviendas con garaje cuestan 2.5829^{4} euros más que las que no tienen, en promedio y controlando por las demás variables.

Punto clave: Estos efectos son diferentes de los que obtendríamos con regresiones simples, ya que aquí hemos “limpiado” la influencia de las otras variables.

La perspectiva geométrica de mínimos cuadrados

La estimación por mínimos cuadrados tiene una interpretación geométrica elegante y potente que nos ayuda a comprender qué está ocurriendo.

Podemos pensar en el vector de observaciones \(\mathbf{y}\) como un punto en un espacio de \(n\) dimensiones. Las columnas de la matriz de diseño \(\mathbf{X}\) generan un subespacio vectorial dentro de \(\mathbb{R}^n\), conocido como el espacio columna de \(\mathbf{X}\), denotado \(C(\mathbf{X})\). Este subespacio contiene todas las posibles combinaciones lineales de nuestros predictores.

El método MCO encuentra el vector de valores ajustados \(\hat{\mathbf{y}} = \mathbf{X}\hat{\boldsymbol{\beta}}\) que está “más cerca” de \(\mathbf{y}\). Geométricamente, este punto no es otro que la proyección ortogonal del vector \(\mathbf{y}\) sobre el subespacio \(C(\mathbf{X})\).

Esta proyección se realiza a través de una matriz especial llamada matriz de proyección o matriz sombrero (hat matrix), denotada por \(\mathbf{H}\):

\[\hat{\mathbf{y}} = \text{Proj}_{C(\mathbf{X})}\,\mathbf{y} = \mathbf{H}\,\mathbf{y}, \qquad \text{donde} \quad \mathbf{H} = \mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\]

Esta operación induce la descomposición ortogonal fundamental del vector de respuesta:

\[\mathbf{y} = \hat{\mathbf{y}} + \mathbf{e}\]

El hecho de que la proyección sea ortogonal implica que el vector de residuos \(\mathbf{e}\) es ortogonal (perpendicular) al vector de valores ajustados \(\hat{\mathbf{y}}\) y, de hecho, a todo el subespacio \(C(\mathbf{X})\). Esta ortogonalidad, \(\hat{\mathbf{y}}^T\mathbf{e}=0\), es la base del Teorema de Pitágoras para la regresión, que permite la descomposición de la variabilidad total en una parte explicada y una no explicada.

3.4 Evaluación del modelo y descomposición de la varianza

Una vez estimado el modelo, el siguiente paso es evaluar su desempeño. ¿Qué tan bien se ajustan nuestras predicciones a los datos reales? Aunque ya vimos la perspectiva geométrica y el Teorema de Pitágoras en regresión simple, es importante revisitar estos conceptos porque en regresión múltiple la interpretación y el cálculo de la descomposición de varianza presenta matices adicionales que debemos entender claramente.

En regresión múltiple, la Descomposición de la Varianza o ANOVA (Analysis of Variance) cobra especial relevancia porque ahora tenemos múltiples variables explicativas y necesitamos evaluar el aporte conjunto de todas ellas, así como su significancia global.

La idea fundamental es que la variabilidad total de la variable respuesta (\(Y\)) puede descomponerse en dos partes: una parte que es explicada por nuestro modelo de regresión (ahora con múltiples variables) y otra parte que queda sin explicar, atribuida al error aleatorio.

Partimos de la identidad: \((y_i - \bar{y}) = (\hat{y}_i - \bar{y}) + (y_i - \hat{y}_i) = (\hat{y}_i - \bar{y}) + e_i\).

Elevando al cuadrado y sumando para todas las observaciones (y gracias a la propiedad de ortogonalidad \(\hat{\mathbf{y}}^T\mathbf{e}=0\), que hace que los productos cruzados se anulen), llegamos a la descomposición fundamental de las sumas de cuadrados:

\[\sum_{i=1}^n (y_i - \bar{y})^2 = \sum_{i=1}^n (\hat{y}_i - \bar{y})^2 + \sum_{i=1}^n e_i^2\]

Esto se conoce como la ecuación de ANOVA:

\[SST = SSR + SSE\]

Donde:

SST (Suma de Cuadrados Total): Es la variabilidad total de \(Y\). Mide la dispersión de los datos observados alrededor de su media.
SSR (Suma de Cuadrados de la Regresión): Es la variabilidad explicada por el modelo. Mide la dispersión de los valores predichos alrededor de la media.
SSE (Suma de Cuadrados del Error): Es la variabilidad no explicada o residual. Mide la dispersión de los datos observados alrededor de la línea de regresión.

Esta tabla no es solo un resumen; es el motor de las principales herramientas de evaluación e inferencia del modelo.

3.4.1 Coeficiente de determinación múltiple

El coeficiente de determinación, \(R^2\), es la medida de ajuste más popular. Responde a la pregunta: ¿Qué proporción de la variabilidad total de Y es explicada por las variables predictoras del modelo?

\[R^2 = \frac{SSR}{SST} = 1 - \frac{SSE}{SST}\]

Propiedades clave:

Su valor siempre está entre 0 (el modelo no explica nada) y 1 (el modelo explica toda la variabilidad).
Puede interpretarse como el cuadrado de la correlación entre los valores observados y los valores predichos, \(R^2 = \text{corr}^2(\mathbf{y}, \hat{\mathbf{y}})\).
Problema: \(R^2\) nunca decrece al añadir una nueva variable predictora al modelo, incluso si esta es completamente irrelevante. Esto lo convierte en una métrica engañosa para comparar modelos con distinto número de predictores.

3.4.2 El coeficiente de determinación ajustado

Para solucionar el problema de \(R^2\), utilizamos el \(R^2\) ajustado, que introduce una penalización por cada variable añadida. Lo hace comparando las varianzas (sumas de cuadrados divididas por sus grados de libertad) en lugar de solo las sumas de cuadrados:

\[R^2_{adj} = 1 - \frac{SSE/(n-p-1)}{SST/(n-1)} = 1 - \frac{\hat{\sigma}^2}{s_Y^2}\]

Donde \(s_Y^2\) es la varianza muestral de \(Y\). El \(R^2_{ajustado}\) solo aumentará si la nueva variable mejora el modelo más de lo que se esperaría por puro azar. Es, por tanto, la métrica preferida para comparar la calidad de ajuste de modelos anidados.

¡Excelente observación! Tienes toda la razón. En la sección de “Inferencia” me centré en los contrastes de hipótesis (el test t y el test F) pero omití una parte igualmente importante que sí estaba en tu Tema 1: la construcción de intervalos de confianza para los parámetros.

Un contraste de hipótesis te da una respuesta de “sí/no” sobre la significancia, pero un intervalo de confianza te ofrece un rango de valores plausibles para el efecto, lo cual es mucho más informativo.

Aquí tienes una versión revisada y ampliada de la sección “Inferencia estadística en el modelo múltiple” que incluye explícitamente los intervalos de confianza, manteniendo el flujo que hemos construido. Puedes reemplazar la sección anterior por esta.

3.5 Inferencia Estadística en el Modelo Múltiple

La estimación nos da los valores de los coeficientes para nuestra muestra, pero la inferencia nos permite usar esos valores para sacar conclusiones sobre los parámetros de la población. ¿Son estos coeficientes “reales” o podrían ser fruto del azar muestral? Para responder, nos basamos en las propiedades distributivas de nuestros estimadores.

3.5.1 Contraste de hipótesis sobre los coeficientes

El test t nos permite decidir si una variable predictora \(X_j\) tiene una relación estadísticamente significativa con \(Y\), después de controlar por el efecto de todas las demás variables en el modelo.

Hipótesis: La hipótesis nula es que el coeficiente es cero en la población (\(H_0: \beta_j = 0\)), lo que implicaría que \(X_j\) no tiene un efecto lineal sobre \(Y\) una vez que se consideran los otros predictores. La alternativa es que el coeficiente es distinto de cero (\(H_1: \beta_j \neq 0\)).
Estadístico de contraste: Construimos el estadístico t, que mide cuántos errores estándar separan nuestro coeficiente estimado del valor nulo (cero). \[\frac{\hat{\beta}_j - \beta_j}{\text{se}(\hat{\beta}_j)} \sim t_{n-p-1}\] Bajo la hipótesis nula, el estadístico que calculamos con nuestra muestra es \(t_{obs} = \hat{\beta}_j / \text{se}(\hat{\beta}_j)\).
Decisión: Comparamos el valor observado \(t_{obs}\) con la distribución t de Student con \(n-p-1\) grados de libertad. Si el p-valor asociado es suficientemente pequeño (normalmente < 0.05), rechazamos la hipótesis nula y concluimos que la variable es un predictor estadísticamente significativo.

3.5.2 Intervalo de confianza para los coeficientes

Mientras que el test t nos da una decisión binaria, el intervalo de confianza nos proporciona un rango de valores plausibles para el verdadero parámetro poblacional \(\beta_j\). Es una herramienta de estimación más informativa.

La estructura del intervalo se basa en la distribución t que acabamos de ver:

\[\text{Estimación puntual} \pm (\text{Valor crítico}) \times (\text{Error estándar})\]

Para un nivel de confianza del \(100(1-\alpha)\%\), el intervalo para \(\beta_j\) es:

\[\hat{\beta}_j \pm t_{\alpha/2, n-p-1} \cdot \text{se}(\hat{\beta}_j)\]

Interpretación: Tenemos una confianza del \(100(1-\alpha)\%\) de que el verdadero valor del parámetro poblacional \(\beta_j\) se encuentra dentro de este rango.
Dualidad con el Contraste de Hipótesis: Existe una relación directa entre el intervalo de confianza y el test t. Si el valor 0 no está incluido en el intervalo de confianza del 95% para \(\hat{\beta}_j\), es matemáticamente equivalente a rechazar la hipótesis nula \(H_0: \beta_j = 0\) con un nivel de significancia \(\alpha=0.05\). Esto nos da dos formas de llegar a la misma conclusión sobre la significancia de un predictor.

3.5.3 Inferencia sobre la significancia global del modelo

El test F evalúa si el modelo en su conjunto tiene poder predictivo. Es decir, contrasta si al menos uno de los predictores tiene una relación significativa con \(Y\).

Hipótesis: La hipótesis nula es que todos los coeficientes de las pendientes son simultáneamente cero (\(H_0: \beta_1 = \beta_2 = \dots = \beta_p = 0\)), frente a la alternativa de que al menos uno es distinto de cero (\(H_1: \text{Algún } \beta_j \neq 0\)).
Estadístico de contraste: El estadístico F se construye a partir de la tabla ANOVA, comparando la varianza explicada por el modelo con la varianza residual, ajustando por sus respectivos grados de libertad. \[F = \frac{\text{Varianza Explicada}}{\text{Varianza No Explicada}} = \frac{SSR / p}{SSE / (n-p-1)}\]
Decisión: Comparamos el valor del estadístico F con una distribución F de Snedecor con \(p\) y \(n-p-1\) grados de libertad. Un p-valor pequeño indica que el modelo es globalmente significativo y que, como conjunto, nuestros predictores explican una parte de la variabilidad de \(Y\) que no es atribuible al azar.

El test F es una herramienta fundamental, ya que representa el primer paso en la validación de cualquier modelo de regresión múltiple.

Interpretación de las pruebas estadísticas

En nuestro ejemplo de viviendas:

Prueba F global:

F(5, 194) = 389.45, p < 0.001
Conclusión: El modelo es globalmente significativo. Al menos una variable predictora tiene una relación real con el precio.

Pruebas t individuales (ejemplos):

Superficie: t = 24.78, p < 0.001 → Significativa
Garaje: t = 10.99, p < 0.001 → Significativa

Intervalos de confianza (95%):

Superficie: [1079, 1265] euros/m²
No incluye el 0, confirma la significancia estadística

Interpretación práctica: Estamos 95% confiados de que el verdadero efecto de la superficie está entre 1079 y 1265 euros por m², controlando por las demás variables.

3.6 Predicción con el modelo múltiple

Una vez que hemos ajustado y validado nuestro modelo, podemos utilizarlo para uno de sus propósitos más poderosos: hacer predicciones para nuevas observaciones. Es fundamental distinguir entre dos objetivos de predicción diferentes, ya que cada uno conlleva un nivel de incertidumbre distinto.

Supongamos que tenemos un nuevo conjunto de valores para las variables predictoras, representado por el vector \(\mathbf{x}_0^T = [1, x_{01}, x_{02}, \dots, x_{0p}]\). La predicción puntual en ambos casos es la misma:

\[\hat{y}_0 = \mathbf{x}_0^T \hat{\boldsymbol{\beta}}\]

Sin embargo, esta estimación puntual está sujeta a error. Para cuantificar esta incertidumbre, construimos dos tipos de intervalos.

3.6.1 Intervalo de confianza para la respuesta media

Este intervalo responde a la pregunta: ¿cuál es el valor promedio de Y para todas las observaciones con las características \(\mathbf{x}_0\)? Su objetivo es acotar la posición de la verdadera (pero desconocida) superficie de regresión poblacional en el punto \(\mathbf{x}_0\).

La incertidumbre aquí proviene únicamente de la estimación de los coeficientes \(\hat{\boldsymbol{\beta}}\). La varianza de esta predicción media es:

\[\text{Var}(\hat{y}_0) = \text{Var}(\mathbf{x}_0^T \hat{\boldsymbol{\beta}}) = \mathbf{x}_0^T \text{Var}(\hat{\boldsymbol{\beta}}) \mathbf{x}_0 = \sigma^2 \mathbf{x}_0^T (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{x}_0\]

Reemplazando \(\sigma^2\) por su estimador insesgado \(\hat{\sigma}^2\), el intervalo de confianza al \(100(1-\alpha)\%\) para la respuesta media \(E[Y|\mathbf{X}=\mathbf{x}_0]\) es:

\[\hat{y}_0 \pm t_{\alpha/2, n-p-1} \cdot \sqrt{\hat{\sigma}^2 \mathbf{x}_0^T (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{x}_0}\]

3.6.2 Intervalo de predicción para una observación individual

Este intervalo responde a una pregunta más ambiciosa: ¿entre qué valores se encontrará la respuesta de una única y nueva observación con las características \(\mathbf{x}_0\)?

Este intervalo debe considerar dos fuentes de incertidumbre:

La incertidumbre sobre la localización de la verdadera superficie de regresión (la misma que en el intervalo de confianza).
La variabilidad aleatoria inherente a una sola observación, que se desvía de la media poblacional (el error \(\varepsilon_0\), cuya varianza es \(\sigma^2\)).

Por esta razón, un intervalo de predicción siempre será más ancho que un intervalo de confianza para el mismo nivel de significancia. La varianza del error de predicción es la suma de las dos fuentes de varianza:

\[\text{Var}(y_0 - \hat{y}_0) = \text{Var}(\varepsilon_0) + \text{Var}(\hat{y}_0) = \sigma^2 + \sigma^2 \mathbf{x}_0^T (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{x}_0\]

El intervalo de predicción al \(100(1-\alpha)\%\) para una observación individual \(y_0\) es:

\[\hat{y}_0 \pm t_{\alpha/2, n-p-1} \cdot \sqrt{\hat{\sigma}^2 \left(1 + \mathbf{x}_0^T (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{x}_0\right)}\]

La diferencia clave es el “+1” dentro de la raíz cuadrada, que representa la varianza de la nueva observación. Visualmente, tanto la banda de confianza como la de predicción son más estrechas cerca del “centroide” de los datos (la media multivariante de los predictores) y se ensanchan a medida que nos alejamos hacia valores más extremos de los predictores.

3.7 Diagnóstico del modelo múltiple

Al igual que en la regresión simple, una vez ajustado el modelo es fundamental realizar un diagnóstico exhaustivo para verificar que los supuestos del modelo lineal se cumplen. La fiabilidad de todas nuestras inferencias (p-valores e intervalos de confianza) descansa sobre la validez de estos supuestos. El proceso sigue basándose en el análisis de los residuos, nuestra ventana a los errores teóricos no observables (Fox y Weisberg 2018; Harrell 2015).

3.7.1 Verificación de los supuestos clásicos

Los supuestos de linealidad, homocedasticidad, normalidad e independencia se verifican con herramientas muy similares a las vistas en el capítulo anterior, por lo que aquí las resumiremos y presentaremos una herramienta adicional para la linealidad.

Normalidad: El gráfico Q-Q de los residuos estudentizados y el test de Shapiro-Wilk siguen siendo las herramientas principales para comprobar que los errores se distribuyen de forma Normal.
Independencia: Para datos de series temporales, el gráfico de residuos contra el tiempo y el test de Durbin-Watson se utilizan de la misma manera para detectar autocorrelación.
Homocedasticidad (Varianza Constante): El gráfico Scale-Location y el test de Breusch-Pagan siguen siendo los métodos de referencia para detectar heterocedasticidad (patrones de embudo en la dispersión de los residuos).

Para la linealidad, el gráfico de Residuos vs. Valores Ajustados sigue siendo la primera herramienta a inspeccionar. Una nube de puntos sin patrones alrededor del cero sugiere que la forma funcional del modelo es globalmente correcta. Sin embargo, en el contexto múltiple, este gráfico podría ocultar una relación no lineal con una variable específica. Para ello, disponemos de una herramienta más precisa.

3.7.1.1 Gráficos de componente más residuo

El gráfico de Componente más Residuo (CPR o Partial Residual Plots) nos permite visualizar la relación entre la variable respuesta y un único predictor \(X_j\), ajustando por el efecto de todos los demás predictores. Para cada predictor \(X_j\), el gráfico muestra:

\[\text{Residuo Parcial} = e_i + \hat{\beta}_j x_{ij} \quad \text{vs.} \quad x_{ij}\]

La pendiente de una línea ajustada a estos puntos es exactamente \(\hat{\beta}_j\). Si la relación es lineal, los puntos deben seguir la línea de regresión. Una desviación sistemática (una curva) sugiere que la relación con esa variable específica no es lineal y que podría necesitar una transformación (p.ej., logarítmica o cuadrática).

Ejemplo práctico: Gráficos de componente + residuo

Los gráficos CPR nos permiten visualizar si la relación de cada predictor con la respuesta es verdaderamente lineal:

# Cargar librerías necesarias
suppressPackageStartupMessages(library(car))

# Gráficos de Componente más Residuo (CPR)
crPlots(modelo, main = "Gráficos de Componente + Residuo")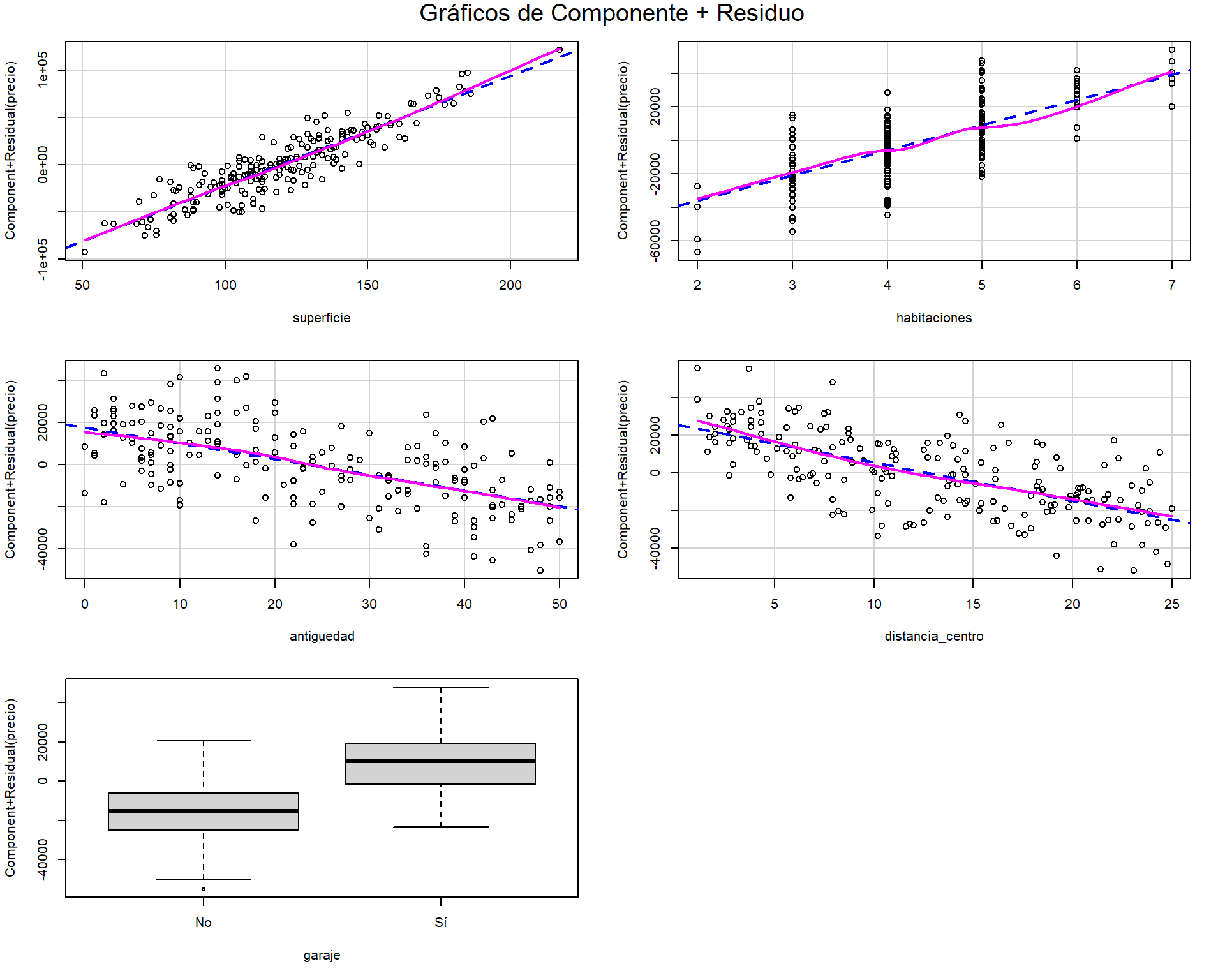

Interpretación:

Línea sólida: Muestra la relación lineal esperada (pendiente = coeficiente de regresión)
Línea punteada: Suavizado no paramétrico de los puntos
Coincidencia de líneas: Sugiere linealidad adecuada
Divergencia significativa: Indica posible no-linealidad que requiere transformación

Si vemos curvas sistemáticas en algún gráfico CPR, es señal de que esa variable podría necesitar una transformación (log, cuadrática, etc.).

3.7.2 Diagnóstico de multicolinealidad

La multicolinealidad es un problema que solo existe en la regresión múltiple. Ocurre cuando dos o más variables predictoras están fuertemente correlacionadas entre sí.

3.7.2.1 Consecuencias de la multicolinealidad

La multicolinealidad no viola los supuestos de Gauss-Markov (los estimadores siguen siendo insesgados y eficientes), pero puede arruinar la interpretación práctica de un modelo:

Varianza de los estimadores inflada: Los errores estándar de los coeficientes de las variables colineales se vuelven muy grandes. Esto dificulta o imposibilita declarar un predictor como estadísticamente significativo, incluso si lo es.
Inestabilidad de los coeficientes: Pequeños cambios en los datos (o añadir/quitar una variable) pueden provocar cambios drásticos en las estimaciones de los coeficientes, incluso cambiando su signo, lo que hace que la interpretación sea poco fiable.
Contradicciones en los contrastes: Se puede dar la paradoja de tener un modelo globalmente significativo (test F con p-valor bajo y \(R^2\) alto) pero con ningún predictor individual significativo (tests t con p-valores altos).

3.7.2.2 Detección de la multicolinealidad

Matriz de correlaciones: Un primer paso es examinar la matriz de correlaciones entre los predictores. Coeficientes de correlación altos (p. ej., > 0.8) son una señal de alerta. Sin embargo, este método no detecta la colinealidad que involucra a tres o más variables.
Factor de Inflación de la Varianza (VIF): Es la herramienta de diagnóstico definitiva. Para cada predictor \(X_j\), se calcula su VIF de la siguiente manera:
1. Se ajusta una regresión lineal de \(X_j\) en función de todas las demás variables predictoras: \(X_j \sim X_1 + \dots + X_{j-1} + X_{j+1} + \dots + X_p\).
2. Se obtiene el \(R^2\) de este modelo auxiliar, que llamamos \(R_j^2\). Este valor nos dice qué proporción de la varianza de \(X_j\) es explicada por los otros predictores.
3. El VIF se calcula como: \[VIF_j = \frac{1}{1 - R_j^2}\]
- Interpretación: El VIF nos dice por qué factor se infla la varianza del estimador \(\hat{\beta}_j\) debido a su relación con los otros predictores.

Reglas prácticas para interpretar VIF

VIF = 1: Ausencia de colinealidad (ideal)
VIF > 5: Valores preocupantes que requieren atención
VIF > 10: Multicolinealidad seria que debe ser tratada

Recordar: El VIF indica por qué factor se multiplica la varianza del coeficiente debido a la multicolinealidad.

Ejemplo: Diagnóstico de multicolinealidad

Caso 1: Sin problemas de multicolinealidad (nuestro modelo actual)

# Calculamos VIF para nuestro modelo de viviendas
vif_values <- vif(modelo)
cat("VIF en nuestro modelo:\n")

VIF en nuestro modelo:

round(vif_values, 2)

      superficie     habitaciones       antiguedad distancia_centro 
            1.40             1.40             1.01             1.01 
          garaje 
            1.01

Como todos los VIF < 5, no hay problemas de multicolinealidad.

Caso 2: Ejemplo con multicolinealidad problemática

# Simulamos un caso con multicolinealidad
set.seed(456)
n <- 100

# Creamos variables altamente correlacionadas
superficie <- runif(n, 50, 200)
habitaciones_sim <- round(superficie/25 + rnorm(n, 0, 0.5))  # Muy correlacionada con superficie
metros_cuadrados <- superficie + rnorm(n, 0, 5)  # Esencialmente la misma que superficie
precio_sim <- 1000*superficie + 5000*habitaciones_sim + rnorm(n, 0, 10000)

# Modelo con multicolinealidad
modelo_colineal <- lm(precio_sim ~ superficie + habitaciones_sim + metros_cuadrados)

# VIF del modelo problemático
vif_problematico <- vif(modelo_colineal)
cat("\nVIF en modelo con multicolinealidad:\n")


VIF en modelo con multicolinealidad:

round(vif_problematico, 2)

      superficie habitaciones_sim metros_cuadrados 
           90.96            10.55            76.57

# Matriz de correlaciones para explicar el problema
datos_problema <- data.frame(superficie, habitaciones_sim, metros_cuadrados)
cor_problema <- cor(datos_problema)
cat("\nMatriz de correlaciones:\n")


Matriz de correlaciones:

round(cor_problema, 3)

                 superficie habitaciones_sim metros_cuadrados
superficie            1.000            0.951            0.993
habitaciones_sim      0.951            1.000            0.942
metros_cuadrados      0.993            0.942            1.000

Interpretación: - VIF > 10: Problema serio de multicolinealidad
- La correlación superficie-metros_cuadrados ≈ 1 explica el problema

Soluciones a los problemas de multicolinealidad

Enfrentar la multicolinealidad no siempre significa que debamos alterar el modelo. La solución adecuada depende de la severidad del problema (medido con el VIF) y, sobre todo, del objetivo de nuestro análisis.

No hacer nada: Si el objetivo principal del modelo es la predicción y no la interpretación de los coeficientes individuales, la multicolinealidad no es un problema grave. El modelo en su conjunto puede tener un buen poder predictivo, aunque los efectos individuales de las variables colineales sean inestables. Además, si las variables colineales no son las variables de interés de nuestra investigación, podemos ignorar su multicolinealidad.
Eliminar una de las variables correlacionadas: Esta es la solución más simple y común. Si dos o más variables miden esencialmente el mismo concepto (p. ej., “educación en años” y “nivel educativo alcanzado”), una de ellas es redundante. Se puede eliminar la que tenga menor relevancia teórica o la que, individualmente, tenga una menor correlación con la variable respuesta.
Combinar las variables colineales: En lugar de eliminar información, podemos combinar las variables colineales en un único predictor compuesto. Por ejemplo, si tenemos gasto_en_publicidad_tv y gasto_en_publicidad_radio, podríamos crear una nueva variable gasto_total_en_medios. Para casos más complejos, se pueden utilizar técnicas de reducción de dimensionalidad como el Análisis de Componentes Principales (PCA) para crear un índice que capture la información conjunta de las variables correlacionadas.
Utilizar métodos de estimación alternativos: Si no es posible o deseable modificar los predictores, se pueden usar técnicas de regresión penalizada que están diseñadas para manejar la multicolinealidad.
- Regresión Ridge: Es el método por excelencia para este problema. Añade un pequeño sesgo a las estimaciones de los coeficientes para reducir drásticamente su varianza, produciendo un modelo mucho más estable y fiable.
- Lasso y Elastic Net: Son otras técnicas de regresión penalizada que también manejan bien la colinealidad y, además, pueden realizar selección de variables al hacer que algunos coeficientes sean exactamente cero.
Aumentar el tamaño de la muestra: En algunos casos, la multicolinealidad puede ser un artefacto de una muestra pequeña. Recolectar más datos puede, en ocasiones, reducir la correlación entre los predictores y disminuir la varianza de los coeficientes.

La elección de la estrategia debe ser una decisión meditada, sopesando la simplicidad, la interpretabilidad y la robustez del modelo final.

3.7.3 Identificación de observaciones influyentes

Los conceptos de outlier (residuo grande), leverage (valor atípico en los predictores) e influencia (impacto en el modelo) son los mismos que en regresión simple. Sin embargo, el caso múltiple nos ofrece herramientas de diagnóstico más específicas.

3.7.3.1 DFBETAS: Influencia sobre coeficientes individuales

Mientras que la Distancia de Cook mide la influencia global de una observación sobre todos los coeficientes a la vez, los DFBETAS miden el impacto que tiene eliminar la observación \(i\) sobre cada coeficiente \(\beta_j\) individualmente.

\[\text{DFBETA}_{j,i} = \frac{\hat{\beta}_j - \hat{\beta}_{j(-i)}}{\text{se}(\hat{\beta}_{j(-i)})}\]

Un DFBETA grande para el coeficiente \(\beta_j\) indica que la observación \(i\) tiene un fuerte poder de atracción sobre la estimación de ese coeficiente en particular. Una regla común es considerar problemáticos los puntos con \(|\text{DFBETA}_{j,i}| > \frac{2}{\sqrt{n}}\).

3.7.3.2 Gráficos de regresión parcial

Estos gráficos son una de las herramientas visuales más potentes y elegantes de la regresión múltiple. Un gráfico de regresión parcial para un predictor \(X_j\) nos permite ver su relación con la respuesta \(Y\) después de haber eliminado el efecto lineal de todos los demás predictores.

Se construye de la siguiente forma: 1. Se calculan los residuos de la regresión de \(Y\) en función de todos los predictores excepto \(X_j\). Llamemos a estos residuos \(e_{Y|X_{-j}}\). 2. Se calculan los residuos de la regresión de \(X_j\) en función de todos los demás predictores. Llamemos a estos residuos \(e_{X_j|X_{-j}}\). 3. Se grafica \(e_{Y|X_{-j}}\) (eje Y) contra \(e_{X_j|X_{-j}}\) (eje X).

Propiedad clave de los gráficos de regresión parcial

La magia de este gráfico: La pendiente de la línea de regresión ajustada a estos puntos es exactamente el coeficiente de regresión múltiple \(\hat{\beta}_j\).

Esta equivalencia matemática es lo que hace que estos gráficos sean tan poderosos para entender la interpretación de los coeficientes en regresión múltiple.

Estos gráficos son útiles para:

Visualizar la magnitud y significancia del efecto de una variable “ajustada”.
Detectar no-linealidades en la relación parcial de una variable.
Identificar observaciones que son influyentes para la estimación de un coeficiente específico (puntos con alto leverage o residuos grandes en este gráfico parcial).

Ejemplo: Gráficos de Regresión Parcial

Los gráficos de regresión parcial nos permiten visualizar la relación “limpia” entre cada predictor y la variable respuesta:

# Gráficos de regresión parcial para todas las variables
avPlots(modelo, main = "Gráficos de regresión parcial")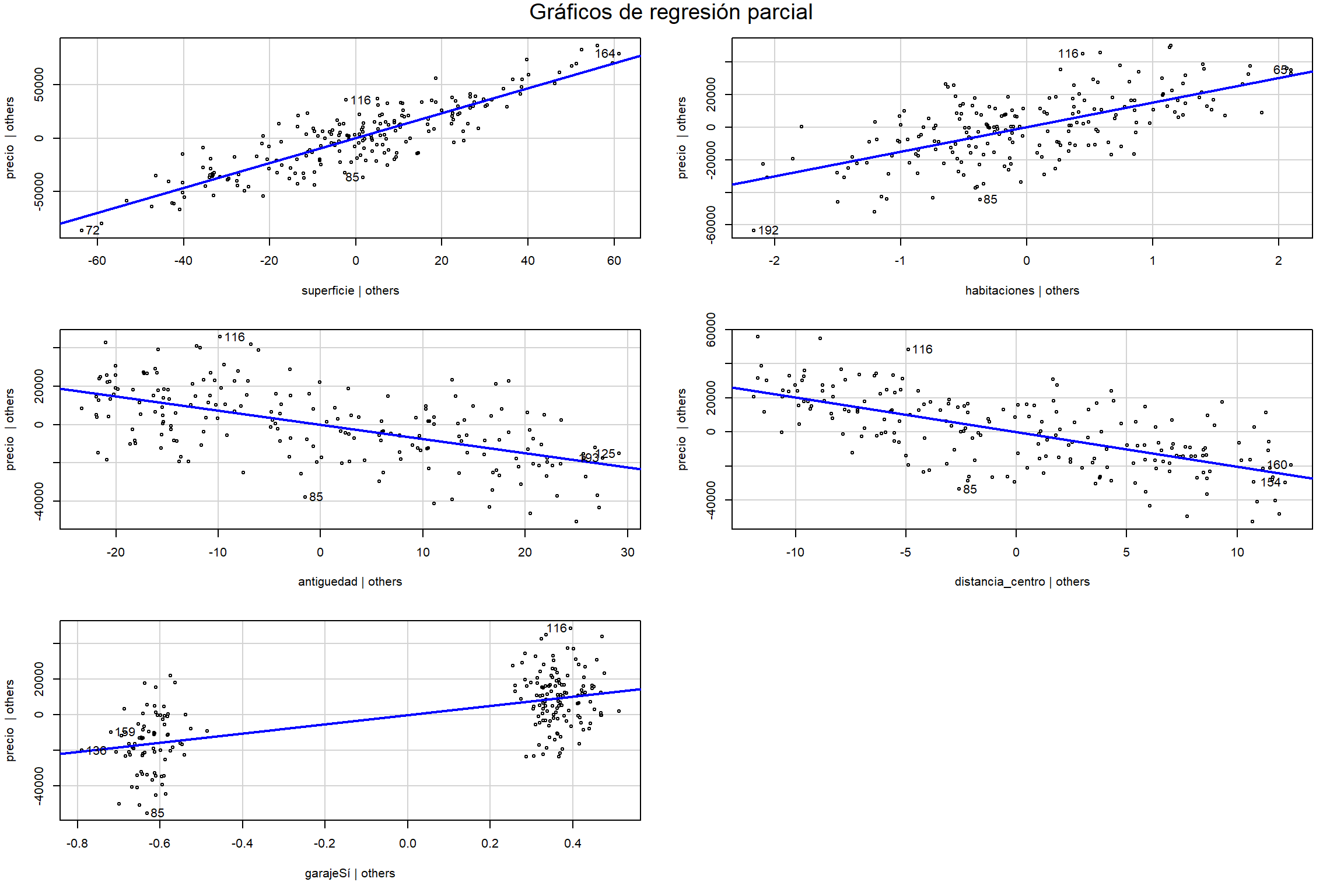

¿Qué vemos en cada gráfico?

Eje X: Residuos de la regresión de \(X_j\) vs. todos los demás predictores
Eje Y: Residuos de la regresión de \(Y\) vs. todos los demás predictores (excepto \(X_j\))
Pendiente: Es exactamente el coeficiente \(\hat{\beta}_j\) del modelo múltiple
Puntos alejados: Observaciones influyentes para ese coeficiente específico

Interpretación práctica: - Una relación lineal clara confirma la validez del modelo - Puntos muy alejados de la línea pueden ser observaciones influyentes - Patrones curvos sugieren no-linealidad en esa variable específica